✏️ Core Example
This example is drawn from the slides and is helpful for multipart problems in this chapter. It is especially helpful when there are two possible outcomes - generally a good outcome and a bad outcome.
✏️ Fill in each of the numbers in the following tables. Assume that the risk free rate is 5% and that the firm borrows $15K. The firm only lasts for one year and the unlevered cost of capital (AKA the cost of capital for unlevered equity) is 15%. The Weak and Strong demand scenarios are equally likely.
| Demand | FCF | Unlevered Equity | Debt | Levered Equity |
|---|---|---|---|---|
| Weak | $27,000 | |||
| Expected | $34,500 | |||
| Strong | $42,000 |
| Demand | % Unlevered Equity | % Debt | % Levered Equity |
|---|---|---|---|
| Weak | |||
| Expected | |||
| Strong |
✔ Scroll down to see the answer.
First we do Unlevered Equity. If there is no debt, the unlevered equity gets all of the cash flows. The unlevered equity has no additional value because the corporation dissolves after 1 year.
| Demand | FCF | Unlevered Equity | Debt | Levered Equity |
|---|---|---|---|---|
| Weak | $27,000 | $27,000 | ||
| Expected | $34,500 | $34,500 | ||
| Strong | $42,000 | $42,000 |
Because the firm has FCF of $27,000, it can borrow $15,000 risk free. This is because it will only need to pay back $15,000*(1+5%) = $15,750 in one year. Therefore, the value of the debt in one year will be the money that it entitles the bearer to:
| Demand | FCF | Unlevered Equity | Debt | Levered Equity |
|---|---|---|---|---|
| Weak | $27,000 | $27,000 | $15,750 | |
| Expected | $34,500 | $34,500 | $15,750 | |
| Strong | $42,000 | $42,000 | $15,750 |
Equity is always the residual claimant. It gets the cash flows after the debt holders have been paid off:
| Demand | FCF | % Unlevered Equity value at T=1 | % Debt value at T=1 | % Levered Equity value at T=1 |
|---|---|---|---|---|
| Weak | $27,000 | $27,000 | $15,750 | $27,000 - $15,750 = $11,250 |
| Expected | $34,500 | $34,500 | $15,750 | $34,500 - $15,750 = $1,8750 |
| Strong | $42,000 | $42,000 | $15,750 | $42,000 - $15,750 = $26,250 |
Now we can move on to the second table. Let’s start on the right. Because the debt is risk free, it’s return is always 5%
| Demand | % Unlevered Equity | % Debt | % Levered Equity |
|---|---|---|---|
| Weak | 5% | ||
| Expected | 5% | ||
| Strong | 5% |
What is the actual % return on Unlevered Equity? Note that the problem tells you the cost of capital for unlevered equity. This is the expected return for Unlevered equity. However, what is the actual return based on whether demand is actually weak or strong?
The Unlevered equity starts out with a value of $30,000. Because we have the return to unlevered equity, we can calculate the T=0 value of the unlevered equity using PDV, based on the T=1 FCF:
The future value of the levered equity is equal to the cash flows, as described above. Therefore, we can calculate the returns to levered equity using our standard IRR formula for %-growth:
| Demand | % Unlevered Equity | % Debt | % Levered Equity |
|---|---|---|---|
| Weak | $27,000/$30,000-1 = -10% | 5% | |
| Expected | $34,500/$30,000-1 = 15% | 5% | |
| Strong | $42,000/$30,000-1 = 40% | 5% |
To calculate the percent return on Levered Equity, we must calculate the value of the levered equity at T=0. Using MM1 to calculate the T=0 value of levered equity should be your first instinct in this chapter.
MM1: (all values at T=0)
To calculate the value of the levered equity at T=0, we subtract D from both sides (ignoring everything before the first ’=‘)
Therefore, the value of the unlevered equity at T=0 is E=V_U−D=$30K −D. If we borrow $15,000, then D = $15,000 and E = $30,000 -$15,000 = $15,000
This assumes that D=$15,000. This is based on our assumption that “Securities are fairly priced.” This is risk-free debt that will return $15,000*1.05 in a year, so it’s current value is $15,000.
It may be helpful at this point to summarize the value of various claims on the firm at T=0.
| Value | How did we calculate this? | |
|---|---|---|
| Unlevered Equity | $30,000 | We took the future value of the Unlevered Equity (which was just the FCF) and we discounted it with the cost of capital for the unlevered equity. $34,500/(1+15%)^1 = $30,000.0 |
| Levered Equity | $15,000 | For this we had to use MM1: E = VU - D = $30,000 - $15,000 = $15,000 |
| Debt | $15,000 | This is how much we borrowed. |
Once you have T=0 values and T=1 values, calculating the return on an asset is fairly straightforward. (T=1 values are given by the cash flows the assets receive at T=1)
Using the T=1 values for levered equity that we calculated above, we can calculate the % return on the Levered Equity. We will use the following formulas:
| Demand | % Unlevered Equity | % Debt | % Levered Equity |
|---|---|---|---|
| Weak | -10% | 5% | $11,250/$15,000-1=-25% |
| Expected | 15% | 5% | $18,750/$15,000-1=25% |
| Strong | 40% | 5% | $26,250/$15,000-1=75% |
Note that we have replicated the following table:
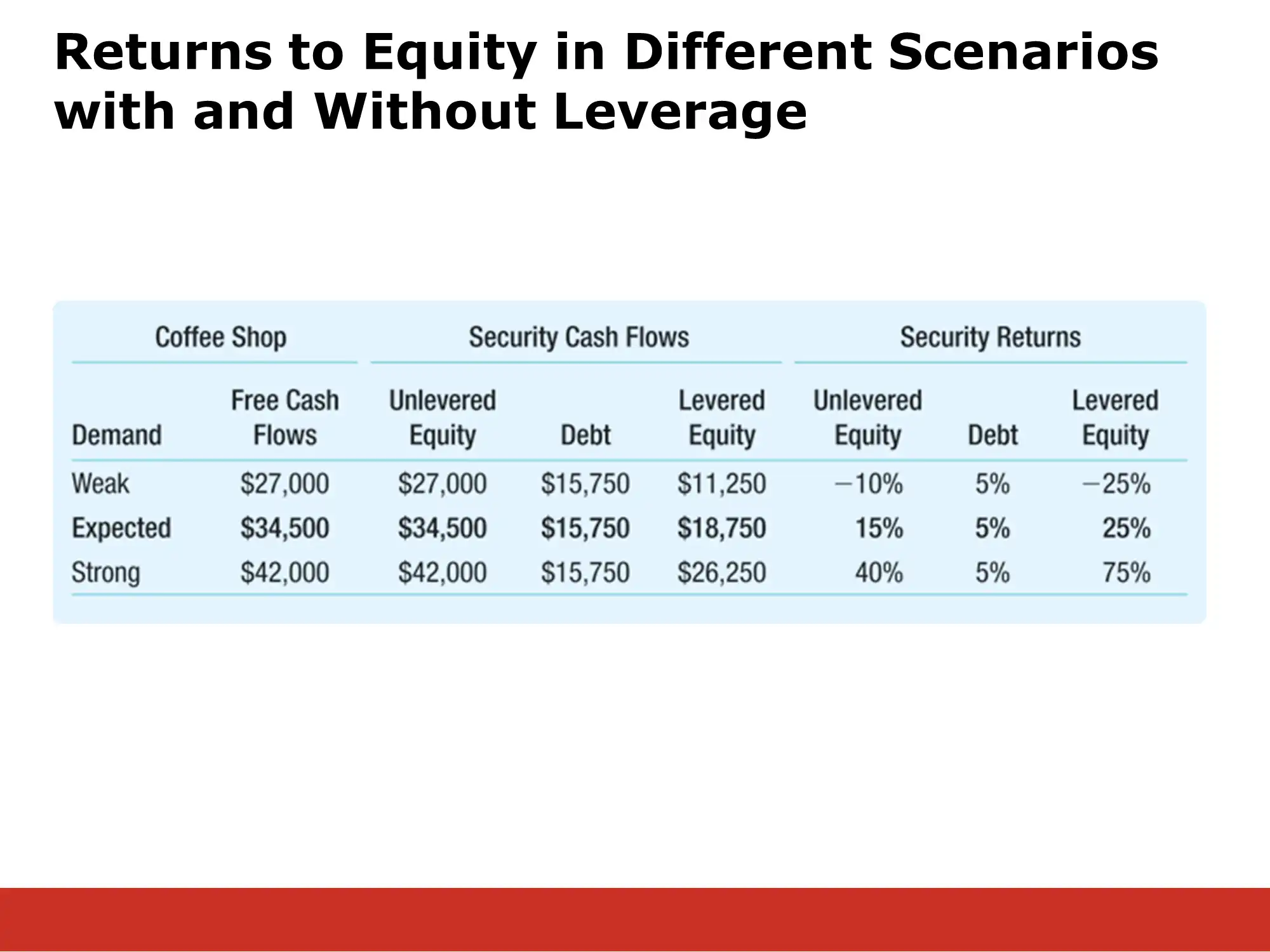
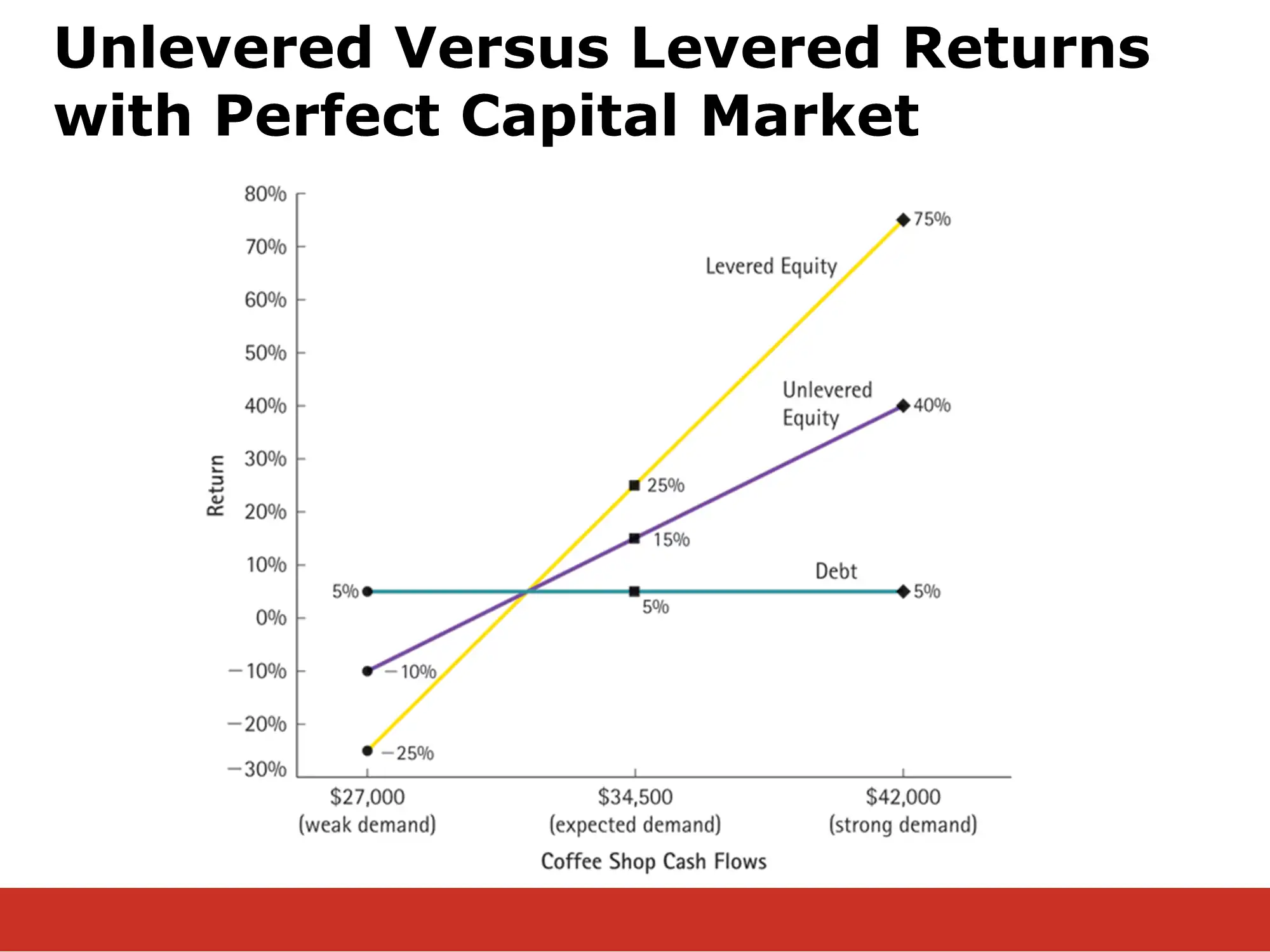
If we graph the % return values, we get the following diagram, which illustrates how risky leverage can be:
Summary of how to calculate the return on the levered equity
To calculate the return on levered equity, we need the initial and final values of the levered equity. Once we have that, we just plug them into our standard formula for return on an asset:
T=0 Value of Levered Equity
For this we use MM1: . MM1 implies,
Therefore, because VU = $30,000, VL = $30,000 - $15,000 = $15,000.
Note that you aren’t given the T=0 value of the unlevered firm, so we must calculate it using PDV:
T=1 Value of Levered Equity
The value of the levered equity at T=1 will be the value of the FCF after the debt has been paid.
| Demand | FCF | Debt value at T=1 | Levered Equity is the “residual claimant” on the FCF |
|---|---|---|---|
| Weak | $27,000 | $15,750 | $27,000 - $15,750 = $11,250 |
| Expected | $34,500 | $15,750 | $34,500 - $15,750 = $18,750 |
| Strong | $42,000 | $15,750 | $42,000 - $15,750 = $26,250 |
Putting these together, we get a expected return (cost of capital) for the levered equity of: